Leveraging Self-Supervision for
Cross-Domain Crowd Counting

Weizhe Liu^1,2, Nikita Durasov¹, Pascal Fua¹,

¹Computer Vision Laboratory, EPFL ²Tencent AI Lab

Abstract

State-of-the-art methods for counting people in crowded scenes rely on deep networks to estimate crowd density. While effective, these data-driven approaches rely on large amount of data annotation to achieve good performance, which stops these models from being deployed in emergencies during which data annotation is either too costly or cannot be obtained fast enough.

One popular solution is to use synthetic data for training. Unfortunately, due to domain shift, the resulting models generalize poorly on real imagery. We remedy this shortcoming by training with both synthetic images, along with their associated labels, and unlabeled real images. To this end, we force our network to learn perspective-aware features by training it to recognize upside-down real images from regular ones and incorporate into it the ability to predict its own uncertainty so that it can generate useful pseudo labels for fine-tuning purposes. This yields an algorithm that consistently outperforms state-of-the-art cross-domain crowd counting ones without any extra computation at inference time.

Video

Cross-Domain Crowd Counting

Crowd Counting (CC) is the task of estimation the number of people presented in an image and it plays an important role for many practical applications such as video surveillance and traffic control. At the same time, most of the techniques developped for CC require significantly large and diverse datasets for training.

Often collecting such a data is impossible and therefore other less data-intensive methods should be used. One of the possible solutions is Cross-Domain methods that can operate both on synthetic and real-world images and therefore amplyfying final accuracy of the model.

Uncertainty Estimation and Masksembles

The ability of deep neural networks to produce useful predictions is now abundantly clear but assessing the reliability of these predictions remains a challenge. The goal of Uncertainty Estimation (UE) is to produce a measure of confidence for model predictions.

In this work, we are using Masksembles layer that pre-generates a set of binary masks before training a network and drops out network's weights in controllable manner during training and inference. In such a way, Masksembles offers number of configurable parameters that allow one to span the whole spectrum of methods between Single Model, MC-Dropout and Ensembles approaches.

Masksembles transformation from Single Model to Ensembles

Self-Supervised Learning for Crowd Counting

Self-Supervised Learning is a machine learning method that allows learning from unlabelled data. In our case, we implement this technique via two-step procedure: 1) given a large-scale dataset of synthetic images with generated (crowd-)labels, we train the network with incorporated Masksembles layer in order to enable uncertainty estimation for it 2) Given the model trained on synthetic data, we run inference for this model on real data and using provided uncertainties we filter only the most confident predictions, add them to training dataset and then retrain the model.

Running this procedure for predefined number of iterations or until convergence, we acquire a model that absorbed information both from synthetic (images + labels) and real (images) data and significantly outperforms other approaches.

Results

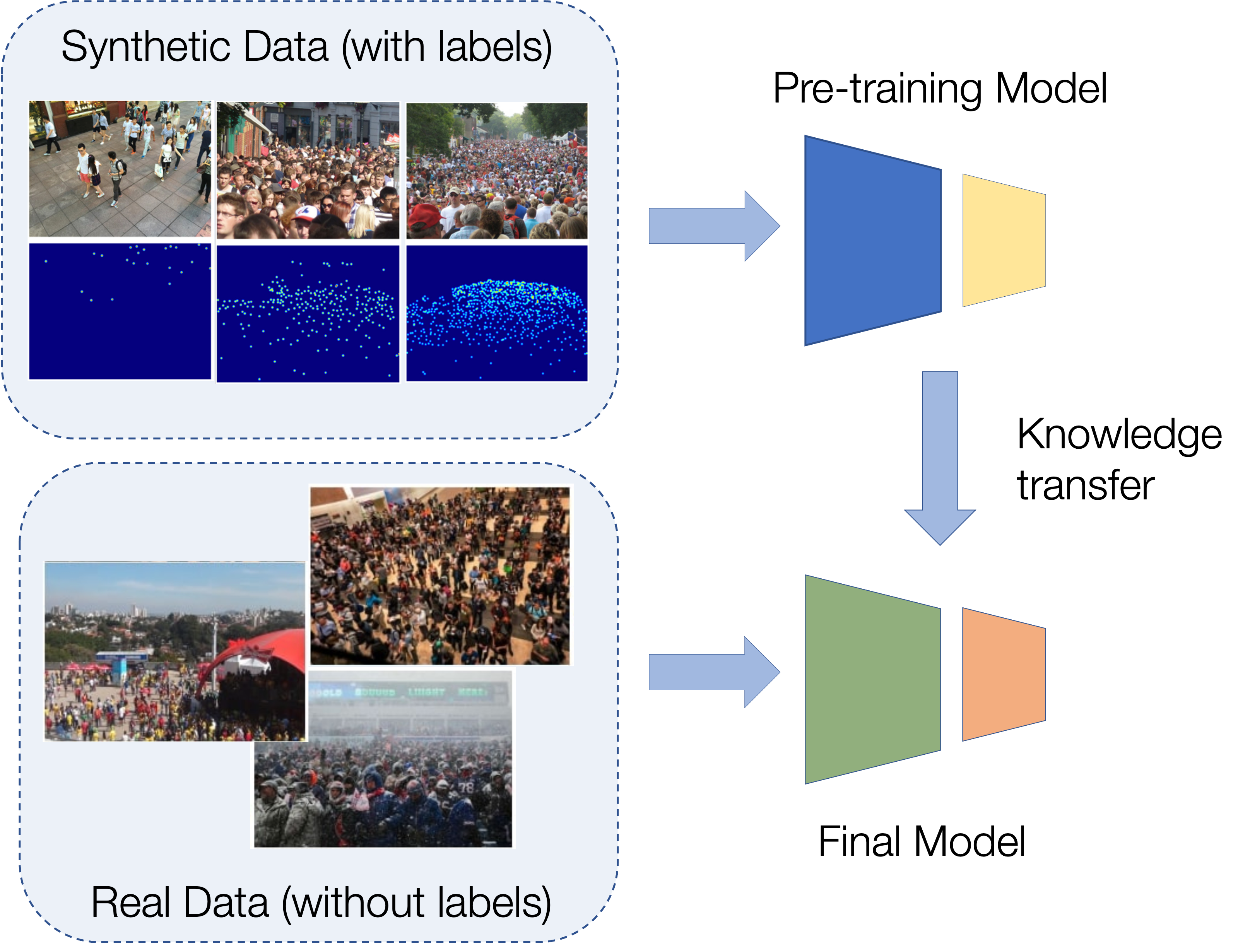
In this section, we introduce benchmark datasets we use in our experiments: 1) large-scale synthetic dataset GCC is used for training, other datasets 2) ShanghaiTech 3) UCF CC 50 4) WorldExpo’10 are used for testing with the same experimental protocols as in earlier [work]. We compare our approach (OURS) to state-of-the-art methods, namely: 1) Cycle-GAN 2) SE Cycle-GAN 3) SE Cycle-GAN (JT) 4) SE+FD 5) GP. "No Adapt" stands for the protocol when one trains the model only on synthetic data and applies it on the real without any adaptation.

Results 1: For ShanghaiTech (Part A and B) and UCF CC 50, we consistently and clearly outperform all other methods in terms of Mean Absolute Error (MAE) and Root Mean Square Error (RMSE) by significant margin. Moreover, for ShanghaiTech our method demonstrates performance that is very close to supervised learning baseline.

**ShanghaiTech Part A**
Model	MAE	RMSE
No Adapt	160.0	216.5
Cycle-GAN	143.3	204.3
SE Cycle-GAN	123.4	193.4
SE Cycle-GAN(JT)	119.6	189.1
SE+FG	129.3	187.6
GP	121.0	181.0
OURS	109.2	168.1
Supervised	76.3	144.2

**ShanghaiTech Part B**
Model	MAE	RMSE
No Adapt	22.8	30.6
Cycle-GAN	25.4	39.7
SE Cycle-GAN	19.9	28.3
SE Cycle-GAN(JT)	16.4	25.8
SE+FG	16.9	24.7
GP	12.8	19.2
OURS	11.4	17.3
Supervised	11.0	17.1

**UCF CC 50**
Model	MAE	RMSE
No Adapt	487.2	689.0
Cycle-GAN	404.6	548.2
SE Cycle-GAN	373.4	528.8
SE Cycle-GAN(JT)	370.2	512.0
GP	355.0	505.0
OURS	336.5	486.1
Supervised	259.3	407.2

Results 2: As for the previous results, our method shows excellent performance both on UCF-QNRF dataset and on all of the scenes of WorldExpo’10. Once again, OURS beats other counterparts both in terms of MAE and RMSE on all of the data.

**UCF-QNRF**
Model	MAE	RMSE
No Adapt	275.5	458.5
Cycle-GAN	257.3	400.6
SE Cycle-GAN	230.4	384.5
SE Cycle-GAN(JT)	225.9	385.7
SE+FG	221.2	390.2
GP	210.0	351.0
OURS	198.3	332.9
Supervised	198.3	332.9

**WorldExpo’10 (Part 1)**
Model	Scene1	Scene2
No Adapt	4.4	87.2
Cycle-GAN	4.4	69.6
SE Cycle-GAN	4.3	59.1
SE Cycle-GAN(JT)	4.2	49.6
GP	-	-
OURS	4.0	31.9
Supervised	2.7	18.2

**WorldExpo’10 (Part 2)**
Model	Scene3	Scene4
No Adapt	59.1	51.8
Cycle-GAN	49.9	29.2
SE Cycle-GAN	43.7	17.0
SE Cycle-GAN(JT)	41.3	19.8
GP	-	-
OURS	23.5	19.4
Supervised	14.3	16.1

**WorldExpo’10 (Part 3)**
Model	Scene5	Average
No Adapt	11.7	42.8
Cycle-GAN	9.0	32.4
SE Cycle-GAN	7.6	26.3
SE Cycle-GAN(JT)	7.2	24.4
GP	-	20.4
OURS	4.2	16.6
Supervised	4.5	11.2

Results 3: Qualitative comparison: these visualizations depict closeness of predictions generated by our method and ground truth density labels for crowd counting. As one can see, OURS accurately restores information about dense crowds and correctly predicts locations of people in sparse regions, therefore generating precise final crowd counts estimations.

Input Image

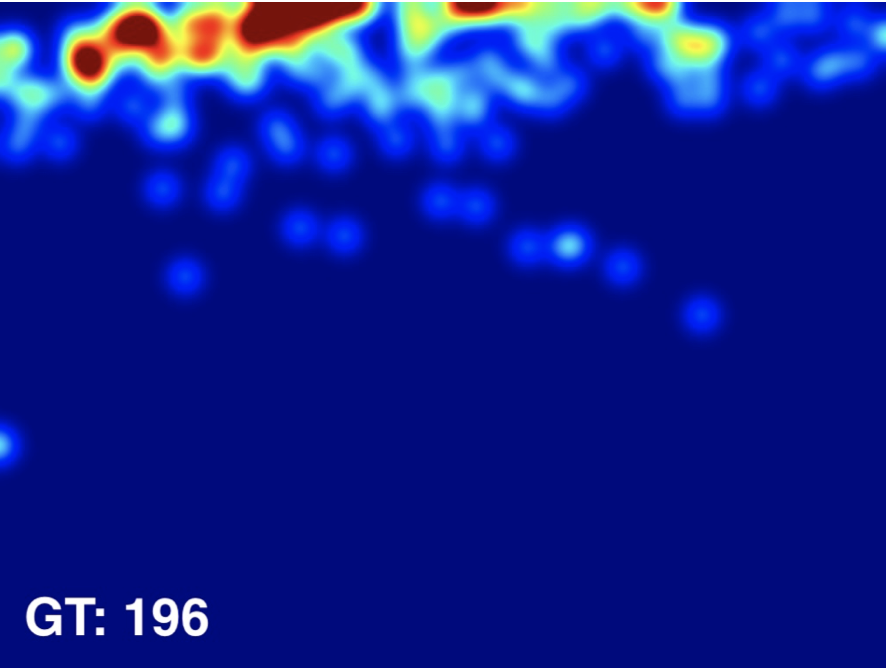
Ground Truth

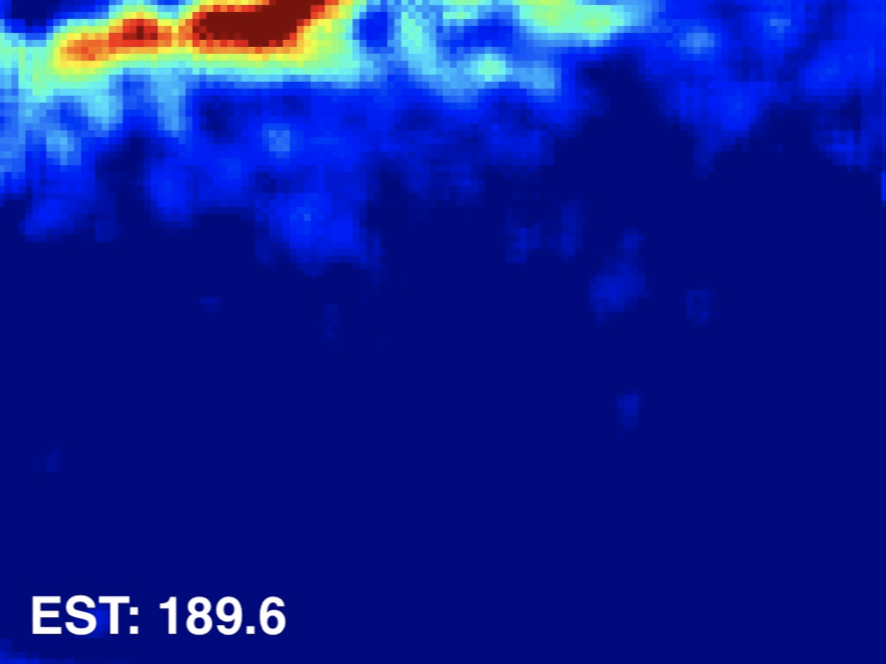
Estimated Density

Input Image

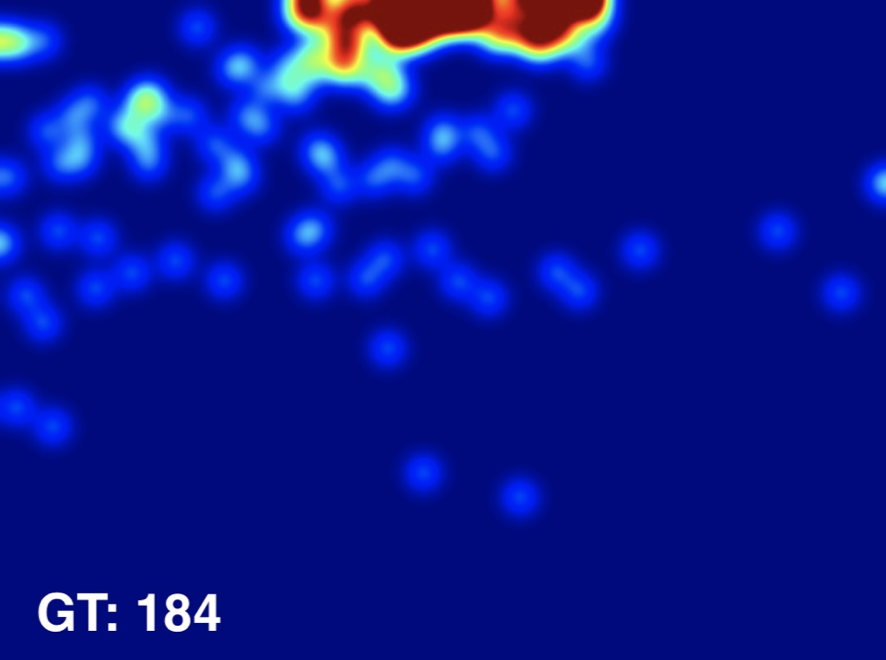
Ground Truth

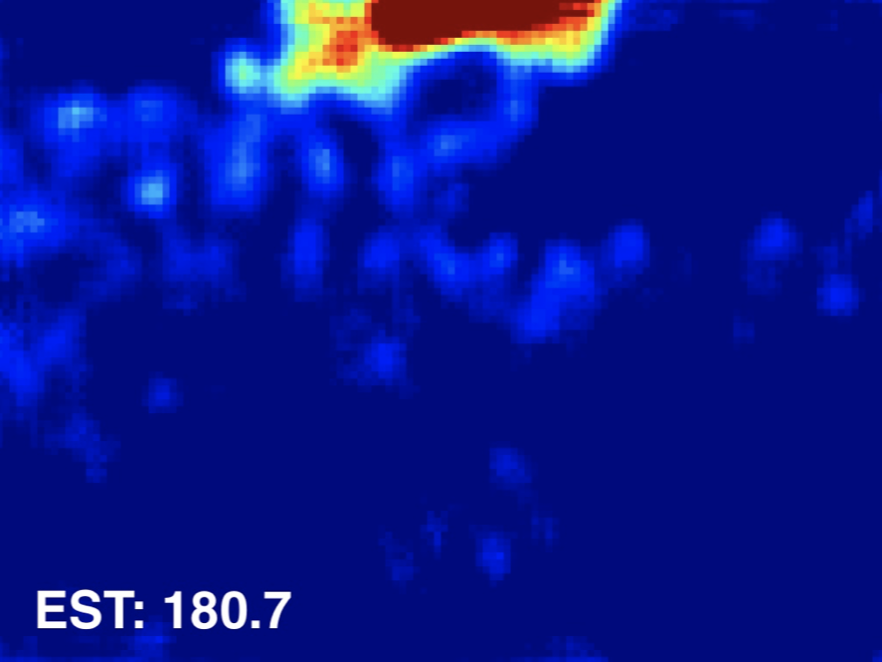
Estimated Density

BibTeX

@inproceedings{liu2022leveraging,
  title={Leveraging Self-Supervision for Cross-Domain Crowd Counting},
  author={Liu, Weizhe and Durasov, Nikita and Fua, Pascal},
  booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
  pages={5341--5352},
  year={2022}   
}